
目次
クラスタリング
手書き数字画像(Scikit-learn付属のdigits)を、教師なしでクラスタリングします。
クラスタリングとは、簡単に言えば、データをグループ分けすることです。
詳しい説明は、自分が理解でするより、こちらのサイトの説明を読むほうがいいと思うので、リンクをのせておきます(笑)。
通常のクラス分類だと、教師データを用意して事前学習します。
でも、クラスタリングはそれを行いません。
なので。
とりあえずデータのグルーピング(分類)のあたりをつけるとかにも使えます。
今回はScikit-learnに付属の手書き画像データ「digits」を使います。
それでクラスタリングをやって、正解の分類とどの程度差があるか?を確認します。
クラスタリングの手法
クラスタリングには色々な手法があります。
データを階層的に分類していく「階層的クラスタリング」の代表的な手法は以下です。
- 最短距離法
- 最長距離法
- 群平均法
- ウォード法
階層を意識せずに評価関数が最適になるように分類していく「非階層的クラスタリング」の代用的な手法は以下です。
- k-means
- Affinity propagation
この中で、圧倒的に露出が多く代表的と言われているのが「k-means」です。
k-meansを使うサンプルソース
k-meansを使って、以下のような手書き数字画像をグルーピングします。

まずは、ソースコードから。
sk_kmean_digits.py
from sklearn import datasets from sklearn import cluster from matplotlib import pyplot as plt # digitsデータのロード digits = datasets.load_digits(n_class=10) # KMeansクラスの生成 model = cluster.KMeans(n_clusters=10) # 学習・クラスタリング実行 model.fit(digits.data) # クラスタリング結果カウント用のリスト初期化 results = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # グラフ表示ラベル用のリスト labels = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'] # グルーピング結果をカウントする for v in model.labels_: results[int(v)] += 1 # 比較用に正解ラベルをカウントするリストの初期化 targets = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # 比較用に正解ラベルをグループごとにカウントする for v in digits.target: targets[int(v)] += 1 # グラフ表示のための設定(クラスタリング結果用) plt.subplot(1, 2, 1) plt.xlabel('results') plt.pie(x=results, labels=labels, autopct='%.2f%%') # グラフ表示設定(正解ラベルカウント用) plt.subplot(1, 2, 2) plt.xlabel('targets') plt.pie(x=targets, labels=labels, autopct='%.2f%%') # 結果表示 plt.show()
補足します。
10グループにクラスタリングします。
結果「model.labels_」には以下のようにはいります。
[1 4 4 0 2 3 7 8 9 4 6 6・・・・]
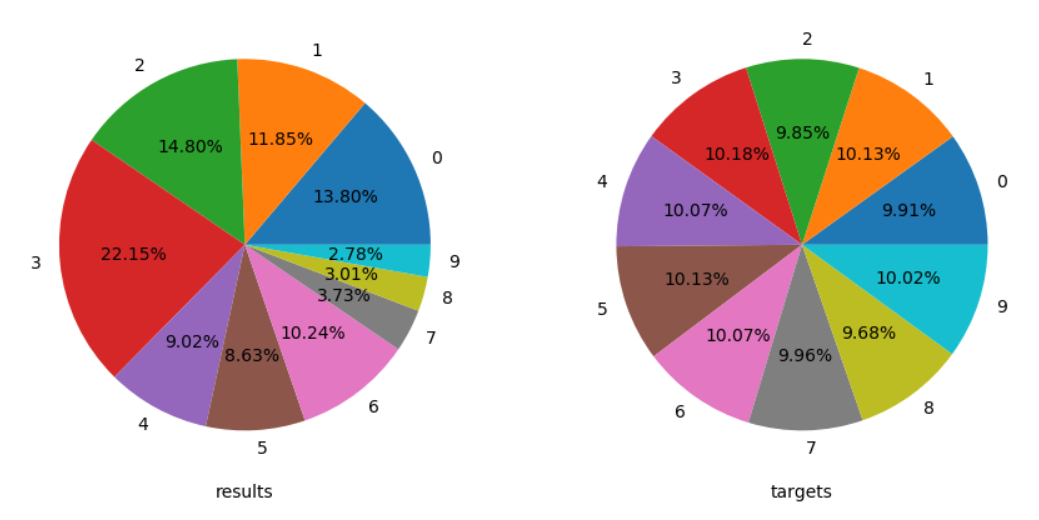
結果のラベルをカウントしたものを円グラフにして、正解の円グラフと比較します。
上(results)がクラスタリングでグループ分け結果で、下(targets)が正解ラベルです。


結構良い感じでグループ分類できているように見えます。
k-means法は、なかなかのものですね。
同じデータとソースを流用して、他の手法を試します。
ソースの変更部分と結果グラフだけを、2つ横並びにで記載します。
グラフは左側がクラスタリング結果、右側が正解です。
ウォード法(階層的クラスタリング)適用結果
k-means法のケースのこの部分を。
model = cluster.KMeans(n_clusters=10)
ウォード法(階層的クラスタリング)だとこう変更して実行します。
model = cluster.AgglomerativeClustering(n_clusters=10, linkage='ward')
sk_agg_ward_digits.py

これはまずまず・・。
群平均法(階層的クラスタリング)適用結果
群平均法(階層的クラスタリング)だとこう変更します。
model = cluster.AgglomerativeClustering(n_clusters=10, linkage='average')
sk_agg_average_digits.py

ちょっと、ブレが大きいかな。
最長距離法(階層的クラスタリング)適用結果
最長距離法(階層的クラスタリング)だとこう変更して実行します。
model = cluster.AgglomerativeClustering(n_clusters=10, linkage='complete')
sk_agg_complete_digits.py
これも結構ブレますね。
最短距離法(階層的クラスタリング)適用結果
最短距離法(階層的クラスタリング)だとこう変更して実行します。
model = cluster.AgglomerativeClustering(n_clusters=10, linkage='single')
sk_agg_single_digits.py 
うーーーん。
全然だめです。
まとめ
あと、Affinity propagation(非階層的クラスタリング)というものもあります。
以下のように指定すれば使えます。
model = cluster.AffinityPropagation()
ただ、Affinity propagationは、k-meansよりも誤差が少ないと言われてますが、クラスタ数を指定せずアルゴリズムが自動的に決定する手法であるため、今回のように10分類に収まらないといけないケースでは使いづらいので、試行から除外しました。
今回の試行では、k-means法を上回る結果の手法はなさそうです。
特に、最後の「最短距離法(single)」は壊滅的ですね(笑)
データと手法があわないと、こうなるんだということは、よーーくわかりました。
クラスタリングでは0に見える数字を0に分類する・・みたいな芸当はできません。
しょせん、アルゴリズムが検出した共通性によってグルーピングしたにすぎなくて、その各グループに対する意味付けは人間がしなければなりません。
でも、だからこそ、使いどころがいろいろあるともいえます。
少なくとも、覚えておいて損はない手法だということは、よくわかりました。
ではでは。