Python3で地球から任意の星までの距離を光年単位で計算する/Pythonサンプル

目次
地球から任意の星までの距離を光年単位で計算する/Python3サンプル
空の星までの距離の計算をPython で実装してみます。
別に計算しなくても、地球から星までの距離の情報はそこかしこにあります。
地球から金星までは「3962万km」。
地球から太陽までは「 1億4709万km」
地球から木星までは「7億4054万km」
などなど。
でも、数字がわかってm、お、こんな途方もない距離をどうやって測るのか?ってとこが気になって仕方ないので、調べてみたわけです。
星までの距離の測り方
Googleで「星までの距離 測り方」と検索すると、いくつか候補がでてきます。
とか。
とか。
どちらにも共通している図がこれです。

三角比ですね。
昔、数学の時間に木の高さを測るという問題で、こんな図をよく見ました。
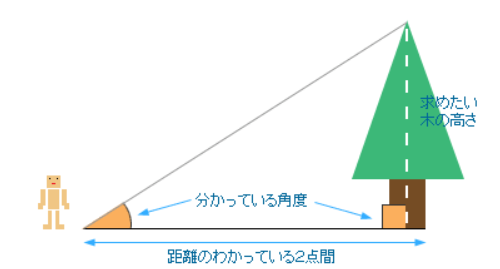
これと同じような考え方です。
三角比の関係を星と地球と太陽の関係に適用するとこうなります。

これを見る限り、P(角度)と太陽と地球の距離がわかれば、星との距離「r」が計算できそうです。
ものの本によれが計算式は「r = R/SinP」だそうです。
太陽と地球の距離(R)は一定ですでにわかっていて、約1億4960万kmです。
次に、角度(P)にあたる部分は、年周視差として求められていて資料があります。
これは度分秒の単位であらわされているので、角度に変換は必要ですが。
なかなか見つけられなかったのですが、探し回って見つけたのが、こちらの表です。
引用すると
- ケンタウルス座アルファ星( α Cen) :年周視差「0.742秒」距離「4.39光年」
- シリウス (α CMa) :年周視差「0.379秒」:距離「8.60光年」
- ベガ (α Lyr): 年周視差「0.123秒」:距離「26光年」
- アルタイル (α Aql): 年周視差「0.194秒」:距離「17光年」
- 北極星 (α UMi) :年周視差「0.00756秒」:距離「430光年」
です。
これを使えば、プログラムにかけるじゃないかということで、やってみます。
年周視差と地球と太陽の距離から距離を光年単位で計算する
Pythonでプログラムを書いてみます。
本当は星の名前を引数にして、内部で年周視差に変換するほうが、スマートなのですが、とりあえず、計算式をPythonに落とし込んで検算したいだけなので、到着して、年周視差を引数にしてクラスを生成すという、実に、ユーザフレンドリーでない仕様になってます(笑)
例によって、ソースから。
import math
class DistanceToStar:
def __init__(self, annual_parallax):
# 年周視差
self.annual_parallax = annual_parallax
# 1度(秒換算)
self.one_degrees = 3600
# 太陽との距離(KM)
self.distance_to_sun_km = 149600000.0
# 1光年の距離(KM)
self.one_light_year_km = 9460730472580.8
def calc(self):
# 年周視差(秒)を角度に換算する
dig = self.annual_parallax / self.one_degrees
# 角度をラジアンにして、Sinを計算する
sin_degrees = math.sin(math.radians(dig))
# 太陽までの距離をSINでわって光年の単位に換算する
return (self.distance_to_sun_km / sin_degrees) / self.one_light_year_km
計算するプログラムの補足
まず、年周視差が「度分秒」単位なので、「角度」に変換してやる必要があります。
度分秒から度への変換をするサイトがあったので、計算式を見てみると、1度=3600秒として、年周視差を3600でわってやれば、角度に変換ができるようです。
ということで、
dig = self.annual_parallax / self.one_degrees
の部分でそれをやってます。
次に、その角度に対する「Sin」を計算します。
math.sinは引数がラジアンなので。
sin_degrees = math.sin(math.radians(dig))
ですね。
あとは、太陽までの距離を、上記のSin値でわって、対象の星までの距離(KM単位)がでるので、それをさらに「1光年」のKM数でわって、光年単位にする。
self.distance_to_sun_km / sin_degrees) / self.one_light_year_km
と・・これで求められるはずです。
計算の実行と答え合わせ
上記のクラスを使って、計算してみました。
d1 = DistanceToStar(0.742) print(d1.calc()) d2 = DistanceToStar(0.379) print(d2.calc()) d3 = DistanceToStar(0.123) print(d3.calc()) d4 = DistanceToStar(0.194) print(d4.calc()) d5 = DistanceToStar(0.00756) print(d5.calc())
その結果がこちらです。
4.395701078995025
8.605831663876279
26.517156102499737
16.812423714472963
431.429920715248
単位はすべて光年です。
こちらの表の5つを表の順番通りに年周視差をあてはめてみましたが、おおよそ、あってますね。

良い感じじゃないでしょうか。
今回はこんなところで。
ではでは。